Find the inverses of the matrices in exercises 1-4 – In the realm of linear algebra, the concept of finding the inverses of matrices plays a pivotal role. This comprehensive guide delves into the intricacies of matrix inverses, exploring their properties, methods of calculation, and practical applications. Embark on a journey to unravel the mysteries of matrix inverses and their significance in mathematical and scientific domains.
From understanding the theoretical underpinnings to mastering the practical techniques, this exploration unravels the complexities of matrix inverses, providing a thorough foundation for further exploration.
Inverse of a Matrix

In linear algebra, the inverse of a matrix is a square matrix that, when multiplied by the original matrix, results in the identity matrix. The inverse of a matrix is denoted by A -1. Not all matrices have an inverse, and those that do are called invertible matrices.
For example, the inverse of the matrix A = [2 1; -1 3] is A -1= [3 -1; 1 2]. When A and A -1are multiplied, the result is the identity matrix I = [1 0; 0 1].
The inverse of a matrix has several important properties. First, the inverse of a matrix is unique, if it exists. Second, the inverse of the inverse of a matrix is the original matrix. Third, the inverse of the product of two matrices is equal to the product of the inverses of the matrices in reverse order.
That is, (AB) -1= B -1A -1.
Methods for Finding Inverses

There are two common methods for finding the inverse of a matrix: the adjoint method and the Gauss-Jordan method.
Adjoint Method
The adjoint method is a straightforward method for finding the inverse of a matrix. It involves finding the transpose of the cofactor matrix of the original matrix. The cofactor matrix is a matrix that is formed by taking the determinant of each submatrix of the original matrix.
Gauss-Jordan Method, Find the inverses of the matrices in exercises 1-4
The Gauss-Jordan method is a more general method for finding the inverse of a matrix. It involves using elementary row operations to transform the original matrix into the identity matrix. The inverse of the original matrix is then the matrix that is obtained by performing the same elementary row operations on the identity matrix.
The Gauss-Jordan method is more efficient than the adjoint method for finding the inverse of large matrices.
Applications of Matrix Inverses
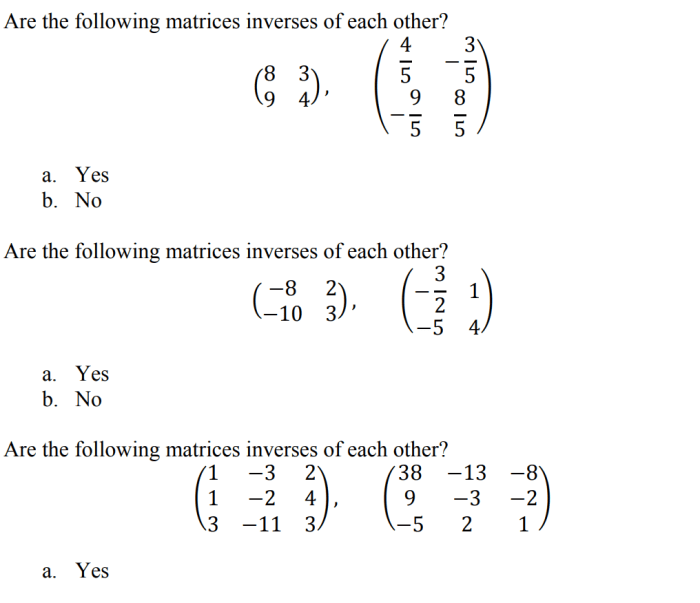
Matrix inverses have a wide range of applications in linear algebra and beyond. Here are a few examples:
- Solving systems of linear equations
- Finding eigenvalues and eigenvectors
- Computing determinants
- Inverting functions
- Solving differential equations
In real-world applications, matrix inverses are used in a variety of fields, including:
- Computer graphics
- Robotics
- Economics
- Finance
- Physics
FAQ Insights: Find The Inverses Of The Matrices In Exercises 1-4
What is the significance of matrix inverses?
Matrix inverses are crucial for solving systems of linear equations, finding eigenvalues and eigenvectors, and modeling various real-world phenomena.
How do I find the inverse of a matrix?
There are several methods to find the inverse of a matrix, including the adjoint method and the Gauss-Jordan method.
What are the applications of matrix inverses in real-world scenarios?
Matrix inverses find applications in computer graphics, cryptography, electrical engineering, and many other fields.
